Changing the Linear Components¶
Here we calculate trends using the SAGE II/OSIRIS/OMPS-LP Dataset. Trends are calculated in the following ways
With two linear terms that have a join point at 1997.
Same as above but with the join point changed to 2000
By fitting ozone anomalies without any linear component, and then fitting the residuals to a linear term
Using two orthogonal forms of the EESC
Start with some imports and loading in the data
[2]:
import xarray as xr
import numpy as np
from LOTUS_regression.regression import regress_all_bins
from LOTUS_regression.predictors import load_data
import LOTUS_regression.predictors.download as download
import LOTUS_regression.plotting.trends as trends
import matplotlib.pyplot as plt
from datetime import datetime
import pandas as pd
import time
[3]:
MERGED_FILE = r'/home/runner/work/lotus-regression/lotus-regression/test_data//S2_OS_OMPS/MERGED_LOTUS.nc'
mzm_data = xr.open_dataset(MERGED_FILE, engine='netcdf4')
We have our default set of predictors which contains linear terms joining at 1997
[4]:
predictors = load_data('pred_baseline_pwlt.csv').to_period('M')
print(predictors.columns)
Index(['enso', 'solar', 'qboA', 'qboB', 'aod', 'linear_pre', 'linear_post',
'constant'],
dtype='object')
And our default set of trends
[5]:
mzm_data = mzm_data.sel(mean_latitude=slice(-60, 60), altitude=slice(10, 50)) # remove bins without data
results = regress_all_bins(predictors, mzm_data['relative_anomaly'], tolerance=0.1)
# Convert to ~ percent
results *= 100
trends.pre_post_with_confidence(results, x='mean_latitude', y='altitude', ylim=(18, 50), log_y=False, figsize=(16, 6),
x_label='Latitude [$^\circ$]', y_label='Altitude [km]', pre_title='Pre 1997',
post_title='Post 1997')
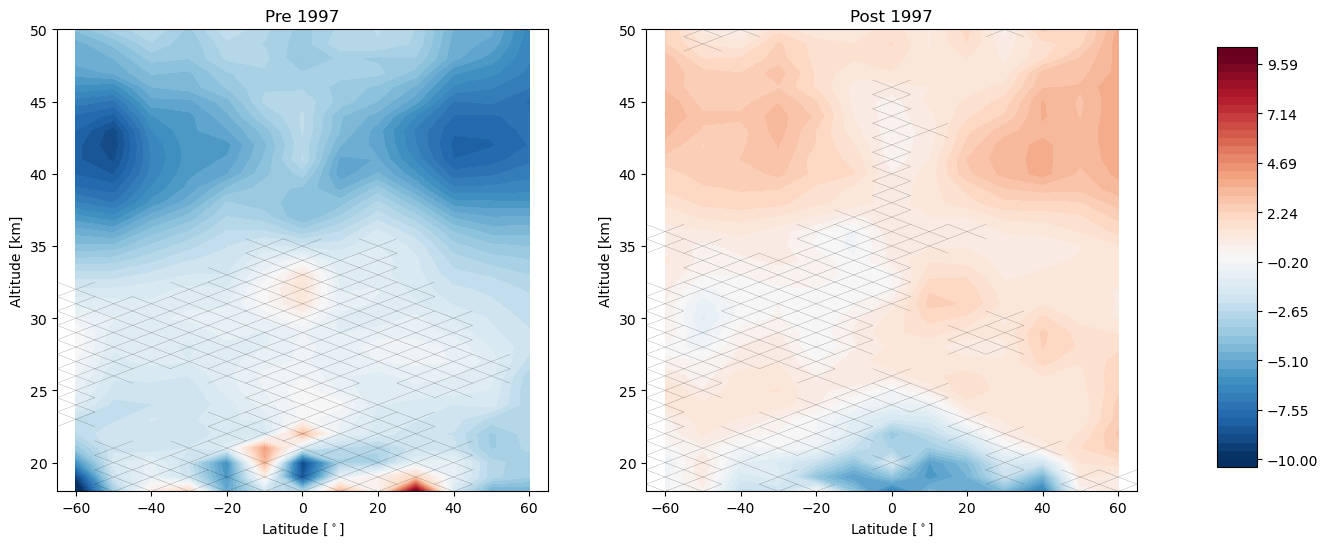
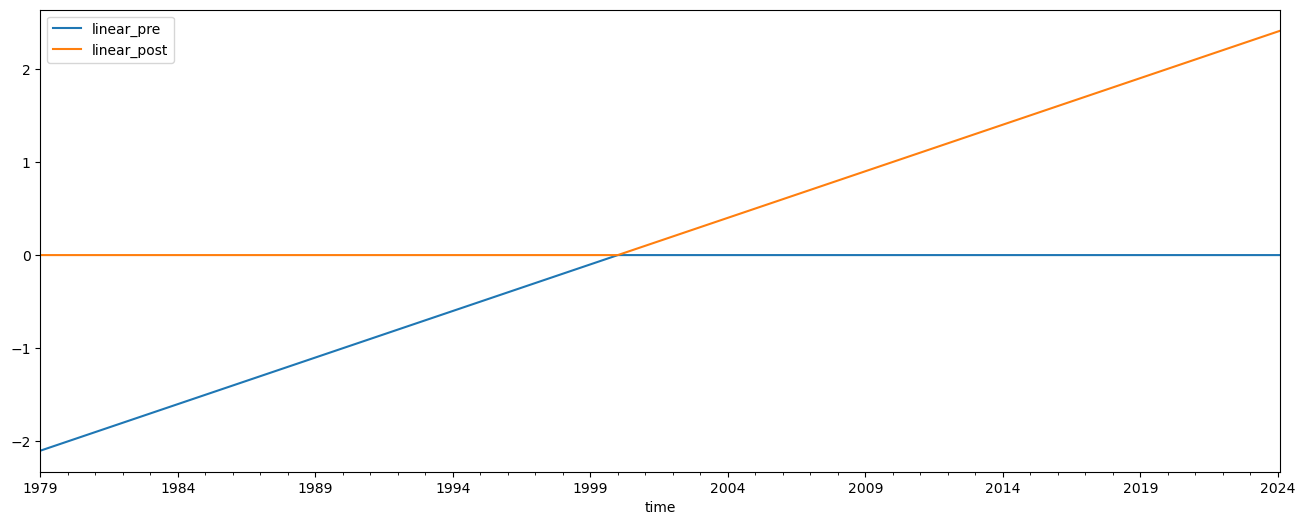
Now we change our inflection point in the linear trend to 2000 instead of 1997, and repeat the analysis
[6]:
predictors[['linear_pre', 'linear_post']] = download.load_linear(inflection=2000)[['pre','post']]
predictors[['linear_pre', 'linear_post']].plot(figsize=(16, 6))
[6]:
<Axes: xlabel='time'>
[7]:
results = regress_all_bins(predictors, mzm_data['relative_anomaly'], tolerance=0.1)
# Convert to ~ percent
results *= 100
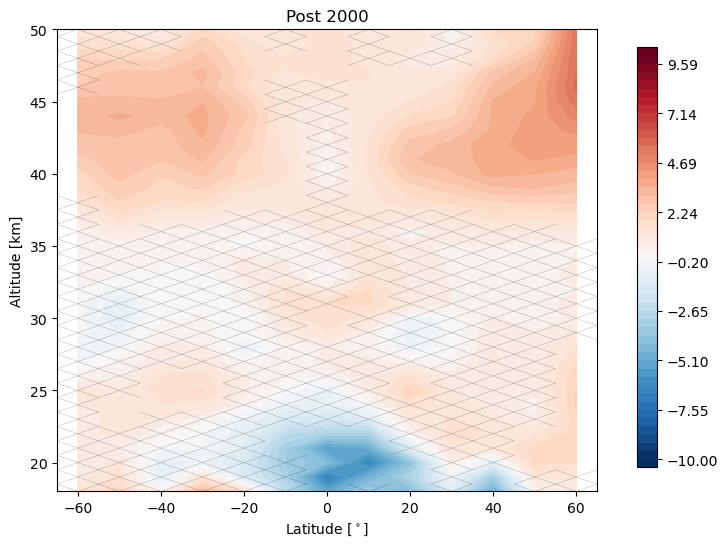
trends.pre_post_with_confidence(results, x='mean_latitude', y='altitude', ylim=(18, 50), log_y=False, figsize=(16, 6),
x_label='Latitude [$^\circ$]', y_label='Altitude [km]', pre_title='Pre 2000',
post_title='Post 2000')
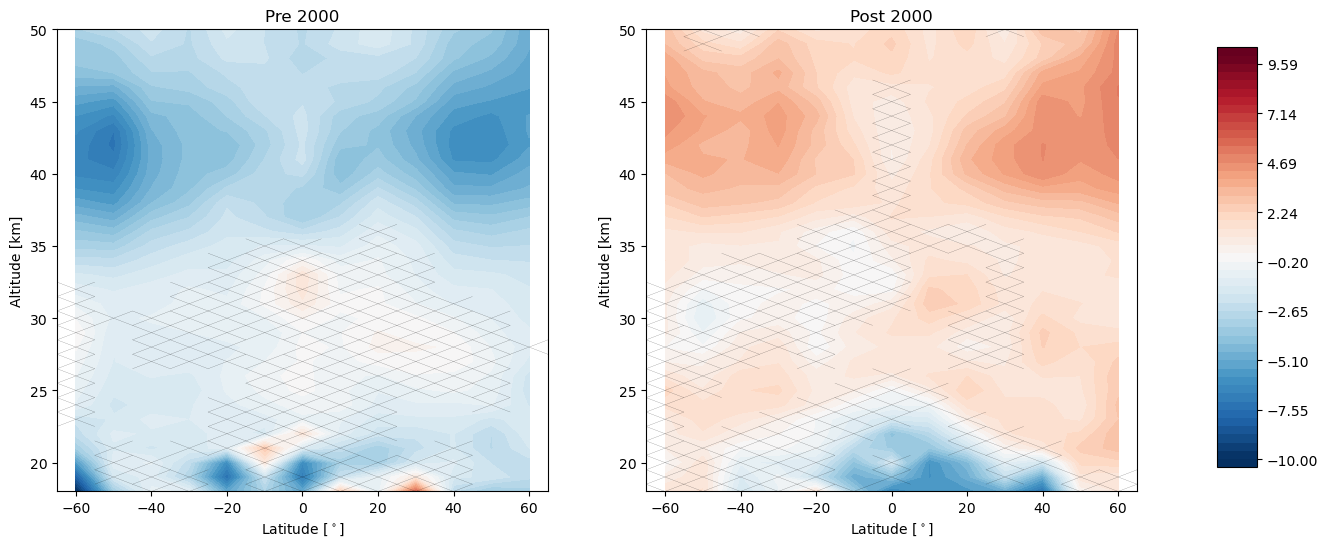
Now we remove the linear terms from our predictors and tell the regression call to post fit a trend to the residuals after the year 2000
[8]:
predictors = predictors.drop(['linear_pre', 'linear_post'], axis=1)
results = regress_all_bins(predictors, mzm_data['relative_anomaly'], tolerance=0.1, post_fit_trend_start='2000-01-01')
# Convert to ~ percent
results *= 100
trends.post_with_confidence(results, x='mean_latitude', y='altitude', ylim=(18, 50), log_y=False, figsize=(8, 6),
x_label='Latitude [$^\circ$]', y_label='Altitude [km]',
post_title='Post 2000')
Lastly we add two orthogonal EESC terms and redo the regression
[9]:
predictors[['eesc_1', 'eesc_2']] = download.load_orthogonal_eesc('/home/runner/work/lotus-regression/lotus-regression/test_data/EESC.txt')[['eesc_1', 'eesc_2']]
predictors[['eesc_1', 'eesc_2']].plot(figsize=(16, 6))
results = regress_all_bins(predictors, mzm_data['relative_anomaly'], tolerance=0.1)
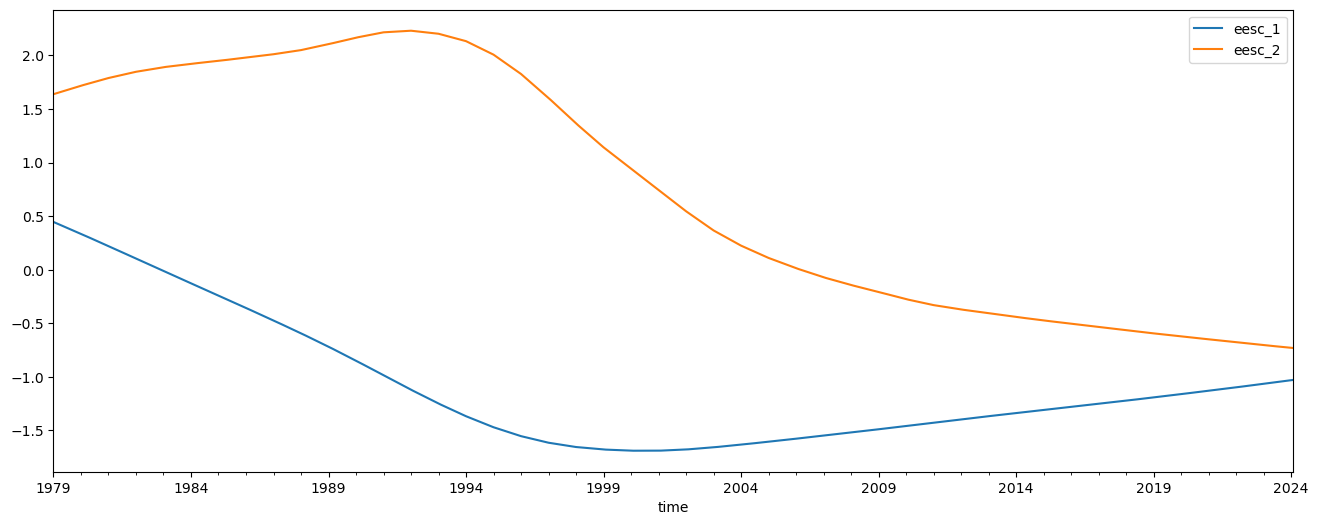
The results are trickier to interpret, but we can combine the two EESC terms to find the total contribution in each bin for the EESC
[10]:
predictors = predictors[(pd.to_datetime(predictors.index.to_timestamp()) >= mzm_data.time.values[0]) & (pd.to_datetime(predictors.index.to_timestamp()) <= mzm_data.time.values[-1])]
eesc_contrib = results['eesc_1'].values[:, :, np.newaxis] * predictors['eesc_1'].values[np.newaxis, np.newaxis, :] +\
results['eesc_2'].values[:, :, np.newaxis] * predictors['eesc_2'].values[np.newaxis, np.newaxis, :]
plt.plot(mzm_data.time.values, eesc_contrib[2, 40, :].T)
np.shape(eesc_contrib)
plt.title('EESC Contribution at 45 S, 40 km')
[10]:
Text(0.5, 1.0, 'EESC Contribution at 45 S, 40 km')
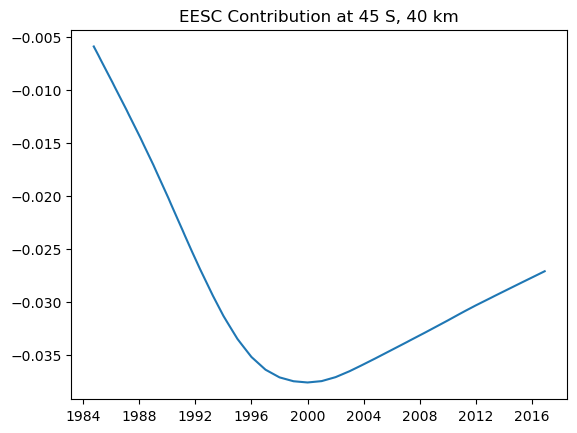
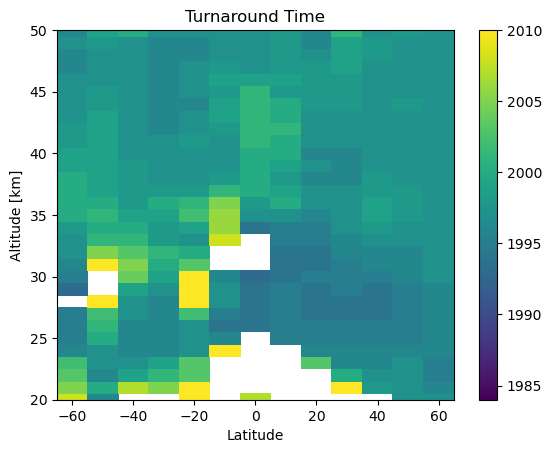
With some annoying time conversions we can also find the predicted turnaround time in each bin
[11]:
turnaround_index = np.argmin(eesc_contrib, axis=2)
turnaround_times = mzm_data.time.values[turnaround_index]
def to_year_fraction(date):
def since_epoch(date): # returns seconds since epoch
return time.mktime(date.timetuple())
try:
ts = (np.datetime64(date, 'ns') - np.datetime64('1970-01-01T00:00:00Z')) / np.timedelta64(1, 's')
except:
print(np.datetime64(date))
return np.nan
dt = datetime.utcfromtimestamp(ts)
s = since_epoch
year = dt.year
startOfThisYear = datetime(year=year, month=1, day=1)
startOfNextYear = datetime(year=year+1, month=1, day=1)
yearElapsed = s(dt) - s(startOfThisYear)
yearDuration = s(startOfNextYear) - s(startOfThisYear)
fraction = yearElapsed / yearDuration
return dt.year + fraction
turnaround_times = np.frompyfunc(to_year_fraction, 1, 1)(turnaround_times).astype(float)
turnaround_times[turnaround_index == 0] = np.nan
turnaround_times[turnaround_index == len(mzm_data.time.values)-1] = np.nan
plt.pcolor(mzm_data.mean_latitude.values, mzm_data.altitude.values, np.ma.masked_invalid(turnaround_times.T))
plt.clim(1984, 2010)
plt.ylim(20, 50)
plt.ylabel('Altitude [km]')
plt.xlabel('Latitude')
plt.title('Turnaround Time')
plt.colorbar()
[11]:
<matplotlib.colorbar.Colorbar at 0x7f4d5f755180>