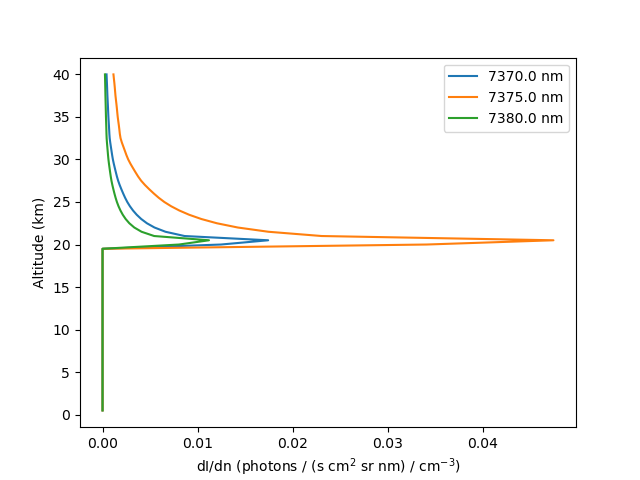
Number Density Weighting Function Calculation

The following example demonstrates the calculation of number density weighting functions at 3 wavelengths for a range of perturbation altitudes (specified by wf_heights).

import sasktran as sk
import sasktran.tir.interface as tir
import numpy as np
import matplotlib.pyplot as plt

# select wavelengths
wavelengths = np.linspace(7370, 7380, 3)

# create a limb line of sight
geometry = sk.VerticalImage()
# NOTE: the VerticalImage class requires sza and saa to be specified but the solar position has no effect
#       on TIR radiance calculations
geometry.from_sza_saa(sza=0, saa=0, lat=45, lon=0, tanalts_km=[20], mjd=56300, locallook=0.0)

# create an atmosphere containing methane; using the TIR engine's builtin climatologies
atmosphere = sk.Atmosphere()
atmosphere.atmospheric_state = tir.ClimatologyAtmosphericState()
atmosphere['CH4'] = sk.Species(tir.HITRANChemicalTIR('CH4'), tir.ClimatologySpecies('CH4'))

# enable methane weighting function calculation
atmosphere.wf_species = 'CH4'

# create the engine
engine = tir.EngineTIR(geometry=geometry, atmosphere=atmosphere, wavelengths=wavelengths)

# weighting function settings
wf_heights = np.arange(500, 40500, 500)
wf_widths = np.ones_like(wf_heights) * 500
engine.options['wfheights'] = wf_heights
engine.options['wfwidths'] = wf_widths

# do the calculation
radiance, weighting_functions = engine.calculate_radiance()

# plot the result
plt.figure()
for i in range(len(wavelengths)):
    plt.plot(weighting_functions[i, 0, :], wf_heights / 1000, label='{} nm'.format(wavelengths[i]))
plt.xlabel('dI/dn (photons / (s cm$^2$ sr nm) / cm$^{-3}$)')
plt.ylabel('Altitude (km)')
plt.legend()

plt.show()